Beckman's World

28 de jun. de 2012

Fiquem ligados, porque aqui o assunto filosofia ferve. Acompanhem mais uma análise dos estudos de Aristóteles no blog Mundo de Beakman.

Estudo do que é Ciência da Natureza (física) para Aristóteles, em sua Obra:
"Segundos Analíticos - Livro II"

No primeiro capítulo do segundo livro da Física Aristóteles fornece uma lista daquilo que seria objeto da ciência da natureza, declarando que todas as outras coisas não dispostas na lista seriam por "outras causas" distintas da natureza.

Nessa lista Aristóteles diz: "Entre os entes, uns são por natureza, outros são por outras causas; por natureza são os animais e suas partes, bem como as plantas e os corpos simples, isto é, terra, fogo, ar e água (de fato dizemos que essas e tais coisas são por natureza), e todos eles se manifestam diferentes em comparação com os que não se constituem por natureza, pois cada um deles tem em si mesmo principio de movimento e repouso -uns, de movimento local, outros, de crescimento e definhamento, outros de alteração.."

*Para os Gregos, Natureza significa "o movimento do mundo" ou seja, as plantas morrendo, nascendo novamente, as águas correndo, etc..

*O objetivo da ciência da natureza (física) é descobrir a causa última!

Para ser ciência da natureza precisa primeiro começar com aquilo que é mais claro para nós e terminar com aquilo que é mais fácil para ser explicado, ou seja, primeiro "para nós" e depois "sem mais".

Ex: "Para nós" -> aquilo que está perto de nós, mas é muito difícil de entender e explicar (amor materno)

"sem mais" -> não pode ser vivenciado mas é mais fácil de ser explicado (triangulo, lua..)

-Tudo que é por natureza se move sozinho e carrega seu sentido de repouso. Existem 3 tipos de movimentos:

~Local: andar, ou se deslocar de um lugar para o outro.

~Crescimento e definhamento: crescer, morrer, apodrecer.

~Alteração: alterações naturais da vida.

Ex: a mudança de cor das folhas das árvores, a mudança da cor dos cabelos para branco, e etc..

*Quando você pinta o cabelo é uma alteração violenta, pois é uma mudança externa.

*Assim como quando a árvore vira mesa também é uma alteração violenta. Quando eu chamo a mesa de mesa ela não é por natureza, mas quando eu a chamo de coisa de madeira ela é por natureza.

*Para Aristóteles, todos os astros (Sol, Lua...) são feitos de Éter, e o movimento das coisas feitas por Éter é ficar girando, e tudo que é feito por éter não é considerado ciência da natureza, pois ele não está incluso nos corpos simples.

26 de jun. de 2012

Aqui faremos uma pequena introdução a este extenso conteúdo que é a trigonometria, se liguem nos próximos posts do Mundo de Beakman que podem ser um complemento deste.

TRIGONOMETRIA

O QUE É?

A Trigonometria (trigono: triângulo e metria: medidas) é o estudo da Matemática responsável pela relação existente entre os lados e os ângulos de um triângulo. Nos triângulos retângulos (possuem um ângulo de 90º), as relações constituem os chamados ângulos notáveis, 30º, 45º e 60º, que possuem valores constantes representados pelas relações seno, cosseno e tangente. Nos triângulos que não possuem ângulo reto, as condições são adaptadas na busca pela relação entre os ângulos e os lados. [1]

A trigonometria tem aplicações importantes em vários ramos, tanto como na matemática pura, quanto na matemática aplicada e, consequentemente, nasciências naturais. A trigonometria é comumente ensinada no Ensino Médio.[2]

HISTÓRIA DA TRIGONOMETRIA

Os estudos iniciais estão relacionados aos povos babilônicos (habitantes da antiga Mesopotâmia, hoje Iraque) e egípcios , sendo desenvolvidos pelos gregos e indianos. Através da prática, conseguiram criar situações de medição de distâncias inacessíveis. Hiparco de Niceia (190 a.C – 125 a.C) foi um astrônomo grego que introduziu a Trigonometria como ciência, este grande astrônomo criou uma matemática aplicada para prever os eclipses e os movimentos dos astros, permitindo a elaboração de calendários mais precisos e maior segurança na navegação. Hiparco ficou conhecido como pai da Trigonometria, por ter estudado e sistematizado algumas relações entre os elementos de um triângulo. O Teorema de Pitágoras possui papel importante no desenvolvimento dos estudos trigonométricos, pois é através dele que desenvolvemos fórmulas teóricas comumente usadas nos cálculos relacionados a situações práticas cotidianas. [1]

Devemos ressaltar que a Trigonometria objetivou a elaboração dos estudos das funções trigonométricas, relacionadas aos ângulos e aos fenômenos periódicos. A partir do século XV, a modernidade dos cálculos criou novas situações teóricas e práticas relacionadas aos estudos dos ângulos e das medidas. Com a criação do Cálculo Diferencial e Integral, pelos cientistas Isaac Newton e Leibniz, a Trigonometria ganhou moldes definitivos no cenário da Matemática, sendo constantemente empregada em outras ciências, como Medicina, Engenharia, Física (ondulatória, óptica), Química, Geografia, Astronomia, Biologia, Cartografia, Navegação entre outras.[1]

SOBRE TRIGONOMETRIA [2]

Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ânguloscorrespondentes são iguais. O fato crucial sobre triângulos semelhantes é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes o maior que o lado do triângulo similar, então o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.

Usando estes fatos, definem-se as funções trigonométricas, começando pelos triângulos retângulos (triângulos com um ângulo reto 90 graus ou π/2radianos). O maior lado em um triângulo qualquer é sempre o lado oposto ao maior ângulo e devido a soma dos ângulos de um triângulo ser 180 graus ou π radianos, o maior ângulo em um triângulo retângulo é o ângulo reto. O maior lado nesse triângulo, consequentemente, é o lado oposto ao ângulo reto, chamado de hipotenusa e os demais lados são chamados de catetos.

Dois triângulos retângulos que compartilham um segundo ângulo $A$ são necessariamente similares, e a proporção (ou razão) entre o comprimento do lado oposto a $A$ e o comprimento da hipotenusa será, portanto, a mesma nos dois triângulos. Este valor será um número entre 0 e 1 que depende apenas de $A$ . Este número é chamado de seno de A e é escrito como $\operatorname{sen}(A)$ . Similarmente, pode-se definir :

o cosseno (ou co-seno) de $A$ : é a proporção do comprimento do cateto adjacente ao ângulo $A$ em relação ao comprimento da hipotenusa
a tangente trigonométrica de $A$ : é a proporção do comprimento do cateto oposto ao ângulo $A$ em relação ao comprimento do cateto adjacente
a co-tangente de $A$ : é a proporção do comprimento do cateto adjacente ao ângulo $A$ em relação ao comprimento do cateto oposto - é o inverso da tangente
a secante trigonométrica de $A$ : é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto adjacente ao ângulo $A$ - é o inverso do cosseno
a co-secante de $A$ : é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto oposto ao ângulo $A$ - é o inverso do seno.

CÍRCULO TRIGONOMÉTRICO
Estudos relacionados à Trigonometria.

O ciclo trigonométrico é uma circunferência de raio unitário com intervalo de [0, 2π], a cada ponto da circunferência associamos um número real. No ciclo trigonométrico trabalhamos três tipos de simetria: em relação ao eixo vertical (seno), eixo horizontal (cosseno) e em relação ao centro. [5]

É uma ferramente de auxílio para o estudo de triângulo retângulo, com seu apoio, torna-se possível definir os ângulos internos do triângulo, que como conhecido, somados devem totalizar 90º ou π/2. As proporções dos três lados do triângulo retângulo são definidas como já ditas de seno, cosseno, tangente e cotagente, dependendo do lado a ser considerado na proporção.
Ficheiro:Circulo Trigonometrico tangente.png

Ficheiro:Circulo Trigonometrico tangente.png

SENO

No círculo trigonométrico, o seno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo vertical, ou seja, no eixo x (abscissas).

Seno é definido como, dado um ângulo conhecido em um triângulo retângulo, o cateto oposto, onde também pode se dizer a aresta oposta, onde os extremos do ângulo considerado não alcançam, a razão deste cateto sobre a hipotenusa (o cateto oposto ao ângulo reto) é igual ao valor do seno do ângulo.

sen = cateto oposto

hipotenusa

COSSENO

No círculo trigonométrico, o cosseno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo horizontal, sendo assim no eixo y (ordenadas).

Cosseno é definido como, dado um ângulo conhecido em um triângulo retângulo é, a proporção do cateto adjascente, agora é cateto onde os extremos do ângulo são limitados (ou toca) pela hipotenusa.

cos = cateto adjascente

hipotenusa

TANGENTE

Em um círculo trigonométrico, a tagente pode ser visualizada como sendo a reta que tangência o círculo, em outras palavras, passando uma reta paralela ao eixo das ordenadas em um ponto equidistante ao centro do círculo de comprimento do seu raio, isto é definido como tangente.

Em trigonometria, a tangente é definida como sendo a proporção do cateto oposto a um ângulo qualquer por seu cateto adjscente, ou seja, podemos defini-lo como a razão do seno pelo cosseno.

tang = cateto oposto = seno

hipotenusa cosseno

TEOREMA DE PITÁGORAS

O Teorema de Pitágoras, é um dos teoremas, senão o mais, conhecido da matemática, aqui vamos definir de forma grosseira este teorema, um dos mais utilizados em trigonometria.

É definido como, “o quadrado da hipotenusa é igual a soma dos quadrados dos catetos”.

Ou seja, dado este seguinte triângulo, onde a hipotenusa tem valo de a e os catetos b,c (letras minúsculas no desenho), o Teorema de Pitágoras ficaria da seguinte maneira

a² = b² + c²

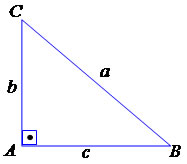
Um corolário desse teorema é que se os dois catetos forem de mesmo tamanho, a hipotenusa vale o produto do cateto pela raiz quadrada de 2. [2]

Por fim, citaremos algumas identidades trigonométricas

IDENTIDADES TRIGONOMÉTRICAS

Algumas equações envolvendo funções trigonométricas são verdade para todos os ângulos e são conhecidas como "identidades trigonométricas". Muitas expressam relações geométricas importantes. Por exemplo, as identidades Pitagoreanas são uma expressão do Teorema de Pitágoras. Aqui há algumas das identidades mais comumente utilizadas, assim como as fórmulas mais importantes conectando ângulos e lados de um triângulo arbitrário.

Fórmula fundamental da trigonometria

sen²A + cos² A = 1
tan²A + 1 = sec²A
1 + cot²A = cosec² A

Soma ou Subtração

sen (A+B) = senAcosB + senBcosA
cos (A+B) = senAsenB + cosAcosB
tang (A+B) = (tangA+tangB)/(1+tangAtanB)
cot (A+B) = (cotAcotB+1)/ (cotB+cotA)

Fórmula da Duplicação do Ângulo

sen(2A) = 2senAcosA
cos(2A) = cos²A – sen²A = 2cos²A-1
cos(2A) = 1-2sen²A = (1-tan²A)/(1+tan²A)
tan(2A)=(2tanA)/(1-tan²A) = (2cotA)/(cot²A-1) = 2/(cotA-tanA)

Fórmula da Divisão de Ângulos

$\begin{align}<br />\operatorname{sen} \frac{A}{2} &= \pm {\sqrt\frac{1-\cos A}{2}} \\<br />\cos \frac{A}{2} &= \pm {\sqrt\frac{1+\cos A}{2}} \\\tan \frac{A}{2} &= \pm \sqrt{\frac{1-\cos A}{1+\cos A}}<br />\end{align}$

LEI DOS SENOS

$\frac{\operatorname{sen} A}{a} = \frac{\operatorname{sen} B}{b} = \frac{\operatorname{sen} C}{c},$
Ou
$\frac{a}{\operatorname{sen} A} = \frac{b}{\operatorname{sen} B} = \frac{c}{\operatorname{sen} C} = 2R$

LEI DOS COSSENOS

$c^2=a^2+b^2-2ab\cos C ,$
Ou
$\cos C=\frac{a^2+b^2-c^2}{2ab}$
e por último, porém não menos importante

LEI DA TANGENTE

$\frac{a+b}{a-b}=\frac{\tan\left[\tfrac{1}{2}(A+B)\right]}{\tan\left[\tfrac{1}{2}(A-B)\right]}$

Referências:
[1] http://www.brasilescola.com/matematica/trigonometria.htm
[2] http://pt.wikipedia.org/wiki/Trigonometria
[3] http://www.mundoeducacao.com.br/matematica/trigonometria.htm
[4] http://pessoal.sercomtel.com.br/matematica/trigonom/trigon1/mod114.htm#trig09
[5] http://www.brasilescola.com/matematica/simetria-no-circulo-trigonometrico.htm
[6] http://www.colegiocatanduvas.com.br/desgeo/trigonometira/

Outro assunto de Filosofia, fiquem espertos nos marcadores caso queiram mais conteúdos dos assunto, se desejam ver a Explicação do Silogismo clique aqui e, continuem acompanhando as atualizações do Mundo de Beakman

Estudo do que é um Silogismo Cientifico para Aristóteles, segundo sua obra:

“Segundos Analíticos – Livro I”

Para um Silogismo ser considerado cientifico segundo Aristóteles, as premissas precisam ter seis características, dadas por ele em sua obra.

-Primeiramente, precisa ser o caso, ou seja, existir e ser verdadeira, pois não da para fazer ciência daquilo que não existe.

-Em segundo, precisa ser primeira, que para ser entendida não necessita de uma explicação anterior.

-Em terceiro; precisa ser imediata, a premissa não pode ter “um meio”, ou seja você não precisa de nenhum conhecimento prévio para entender.

-Em quarto, ela tem que ser mais cognoscível que a conclusão, precisam ser mais óbvias, mais fáceis de aceitar que a conclusão.

-Em quinto, precisam ser anteriores que a conclusão; isto é, você tem que conhecer a causa da consequência, e saber que aquela causa é daquela consequência.
Ex: Madeira -> Mesa
      (causa)         (consequência)

-Em sexto, precisa ser a causa da conclusão, pois para chegar na conclusão são necessários os argumentos utilizados nas premissas.

=> Como ex. de Silogismo cientifico temos este, usado por ele próprio no final de seu livro:
    Todo ser que reflete a luz do sol é lua
    Todo ser que tem o lado luminoso voltado para o sol é ser que reflete a luz do sol
------------------------------------------------------------------------------------------------------------
    Todo ser que tem o lado luminoso voltado para o sol é Lua

Esse silogismo é um silogismo cientifico para Aristóteles, pois ele se enquadra nas 6 características dadas por ele, citadas a cima.

24 de jun. de 2012

Uma matéria mais complexa, assunto de filosofia, o qual se encaixa em nível médio, mas é melhor debatido em nível superior

Explicação do Silogismo feito por Aristóteles, em sua obra: “Analíticos Anteriores”

Um silogismo é constituído de três proposições (termos/frases, que podem ser verdadeiras ou falsas), das duas primeiras, chamadas premissas, concluímos uma terceira, deduzida como a conclusão.

-Os termos podem ter 3 tipos de relações:

1º Um termo dentro do outro:
     Mamífero, Cachorro -> Todos os cachorros são mamíferos.

2º Termos completamente separados:
      Cachorro, Mesa -> Não tem nada a ver.

3º Termos que podem ser relacionados:
     Fêmeas, Cachorro -> Alguns cachorros são fêmeas.

Obs: Esse sistema só da conta para adjetivos e não para ações! (Uma coisa é ou não é a outra)
“Eu sou a favor da vida” não é uma proposição! Pois ela não tem como ser falsa.

-Todas as frases que se adjetivam são apenas de 4 formas:

1º Toda casa é morada (Universal e afirmativo – A/Um termo dentro do outro)
2º Nenhuma casa é morada (Universal negativa – E/Nada a ver)
3º Alguma casa é morada (Particular afirmativa - I/Termos que podem ser relacionados)
4º Alguma casa não é morada (Particular negativa - O/Termos que podem ser relacionados)

Exs: Todo pai é cego                   ->Premissas
       Algum Deus é pai                                                   } Silogismo (Ou teoria da inferência)
--------------------------------
      Algum Deus é cego                ->Conclusão (são válidos ou inválidos, depende da conta)

      Todo elfo é fada
      Todo bicho papão é fada                  } As proposições são todas verdadeiras, mas a conta está
----------------------------------------                 errada, ou seja, a conclusão é falsa.
     Todo elfo é bicho papão

Obs: De contas falsas eu posso gerar um resultado verdadeiro, porém o contrário não pode ocorrer!

-Entimema: É um silogismo em que você esconde uma das premissas, para que fique mais fácil de acreditar na mesma.
Ex: Alguém sai arrumado
      Alguém sai arrumado                      } Premissas particulares
--------------------------------------
Então você também tem que sair arrumado    -> Premissa universal

Ou

Todo prefeito é cidadão, logo todo prefeito vota. (porém nem todo cidadão vota)

Resumo de silogismo

   Premissa 1 ( pode ser v ou f)
   Premissa 2 (v ou f)                           } conhecimento prévio
-------------------------------------
        Conclusão       -> conhecimento
(pode ser v ou f também,
porém é invalida quando não tem lógica)

22 de jun. de 2012

Estreando o tópico Grandes Mentes da Humanidade, iremos falar sobre umas das pessoas mais brilhantes na matemática, considerado por muitos como o "Príncipe da Matemática", o nome dele?

CARL FRIEDRICH GAUSS

QUEM FOI?

Johann Carl Friedrich Gauss, nasceu na Alemanha na cidade de Braunschweig no dia 30 de abril de 1777, morreu no dia 23 de fevereiro de 1855 aos 77 anos na cidade de Göttingen também na Alemanha, foi um matemático, astronômo e físico alemão. Considerado um dos maiores matemáticos de todos os tempos, muitos o condecoram como o "Príncipe da Matemática". Suas contribuições para a ciência é notória, as principais áreas que estudou foram, teoria dos números, estatística, análise matemática, geometria diferencial, geodésia, geofísica, eletroestática, astronomia e óptica.

VIDA

Gauss era filho de pais humildes, mas encontrou apoio de sua mãe e de seu tio para estudar, apesar das objeções paternas. Entrou na escola aos sete anos de idade e logo aos dez segundo a lenda, foi capaz de descobrir a soma dos n primeiros números de uma progressão aritmética (P.A) [veja artigo principal]. Diz a história que sua professora primária para manter a classe ocupada, lhe passou a tarefa de fazer uma soma de 1 a 100, tarefa que Gauss cumpriu quase que de imediato com a utilização da fórmula da PA.

Sn = n(a1 + an )/2

Seu diretor Buttner, ficou pasmo com a genialidade do jovem menino, assim passou a incentivá-lo nos estudos junto com seu assistente de então 17 anos na época Johann Martin Bartels. Entre os dois jovens foi firmada uma grande amizade que perdurou até a morte de Bartels.

Com amigos influentes, Bartels fez com que Gauss conseguisse um pouco de fama, assim foi apresentado ao Duque de Brunswick, Carl Wilhelm Ferdinand,quando tinha 14 anos de idade. O Duque passou a financiar sua educação e posteriormente suas pesquisas científicas além de garantir recursos para a subsistência do célebre matemático.

Em 1792, Gauss ingressou no Collegium Carolinum, onde permaneceu por três anos, estudando as obras mais notáveis de Leonhard Euler, Joseph-Louis de Lagrange e Isaac Newton. É nesse período que Gauss principia suas investigações sobre aritmética superior, que o tornariam imortal e lhe dariam o título de "Príncipe da Matemática".

No ano de 1795, mais especificamente em outubro Gauss deixa o Collegium Carolinum para ingressar na Universidade de Göttingem, em seu primeiro semestre na universidade fez uma brilhante descoberta que o homem buscava a mais de 2000 anos como construir com compasso e esquadro. Esta descoberta foi comemorada com o início de seu diário, que ocorreu mais precisamente no dia 30 de março de 1795, que durante os próximos 18 anos foi testemunha de muitas de suas descobertas. Este diário só foi divulgado 43 anos após a morte de Gauss, quando , para isso, a Sociedade Real de Göttingen obteve a permissão do neto de Gauss. O diário contém 146 anotações, breves exposições dos descobrimentos feitos pelo seu autor no período de 1796 a 1814.. Dentre suas descobertas nos tempos de estudante as mais significativas são a do método dos mínimos quadrados, a prova da reciprocidade quadrática na teoria dos números

Os três anos passados em Göttingen foram dos mais prolíficos de sua vida. As ideias que vinha recolhendo desde os 17 anos, foram, nessa época, ordenadas e esmiuçadas, resultando, em 1798, as Indagações Aritméticas, por muitos considerada a obra-prima de Gauss.

Uma segunda fase da vida de Gauss tem início no primeiro dia do século 19. Giuseppe Piazzi, astrônomo italiano, descobriu um pequeno planeta, Ceres, o primeiro de vários planetas menores hoje conhecidos. A observação do corpo celeste era extremamente difícil, e calcular sua órbita, partindo dos poucos dados obtidos, uma tarefa digna de um gênio. Gauss investigou a órbita, vendo todos os seus cálculos confirmados.

Até a idade de 20 anos Gauss teve um grande interesse por idiomas e quase se tornou um filologista. Posteriormente, literatura estrangeira e leituras sobre política eram seus passatempos, ambos com tendências conservadoras.

Gauss obteve seu doutorado com a defesa de uma tese intitulada NEW DEMOSNSTRATION OF THE THEOREM THAT EVERY RATIONAL INTEGRAL ALGEBRIC FUNCTION IN VARIABLE CAN BE SOLVED INTO REAL FACTORS OF FIRST OR SECOND DEGREE, concluído em 1801.

Aos 28 anos, mais precisamente em 1805, quando atingiu uma condição financeira confortável, já que o duque aumentara sua pensão, Gauss casou-se com Johanne Osthof e, teve com ela três filhos, mas neste mesmo ano o Duque faleceu em combate a Napoleão na Batalha de Jena, e o matemático teve de encontrar um meio de manter sua família. Como sua fama havia espalhado-se pela Europa, Gauss então recebera convite para ocupar a cadeira que um dia teria sido de Leonard Eulel, em São Petersburgo, todavia optou por aceitar a direção do Observatório de Göttingen

Depois do nascimento do terceiro filho, em 1809, sua esposa faleceu. Depois ele se casaria novamente e teria mais tres filhos. Os anos de 1811 e 1812 foram os melhores de sua vida, desfrutando Gauss de certa tranquilidade. Logo após seu segundo matrimônio, foi observado o cometa de 1811 e Gauss teve a satisfação de constatar que o astro seguia exatamente a trajetória por ele calculada.

No período de 1821 a 1848, Gauss foi conselheiro científico dos governos de Hannover e da Dinamarca, completando minuciosos estudos de geodésia, que o levaram a examinar, em toda a sua generalidade, problemas relativos às superfícies curvas e a questão da representação conforme.

PRINCIPAIS OBRAS

EM MATEMÁTICA

Investigando uma questão aparentemente simples - quantos dígitos tem o período de uma decimal periódica? -, Gauss descobre a lei da reciprocidade quadrática e introduz a terminologia das congruências.

Aos 18 anos inventa o método dos mínimos quadrados, indispensável para as medições geodésicas. A Lei de Gauss, relativa à distribuição dos erros, e sua curva normal (em forma de sino) são amplamente conhecidas de todos os que estudam estatística.

Algumas anotações de seu diário mostram que ele descobriu a dupla periodicidade de certas funções elípticas. E outra anotação comprova que ele já havia considerado essa periodicidade no caso geral. Esses descobrimentos, contudo, não chegaram a ser divulgados, não se sabe por qual motivo.

Em 1812, Gauss publica seus estudos sobre as séries hipergeométricas. O interesse de tais séries está em que englobam, como casos particulares, muitas das séries mais notáveis da análise (entre as quais as que permitem cálculo e construção de tabelas de funções trigonométricas, logarítmicas e exponenciais).

Gauss também abriu novos rumos com a invenção de um tipo novo de números, osinteiros complexos gaussianos, da forma a+bi, em que "a" e "b" são inteiros racionais e "i" a unidade imaginária.

Gauss possuía, ainda, grande habilidade manual. Inventou o heliótropo; aperfeiçoou alguns instrumentos de observação, utilizados na astronomia; inventou o magnetômetro bifilar; e descobriu o telégrafo elétrico.

EM FÍSICA

Após a metade da década de 1820 Gauss se rendeu às pressões financeiras, e aos problemas de saúde e de família. Os estudos de Gauss tiveram seu início formal em 1829 com estudos sobre o campo magnético terrestre, porém Gauss mostrou pouca experiência para realizar medições, o que tornou valiosa a colaboração de Weber, um jovem e brilhante fisico. Em outubro deste ano Gauss voltou-se a estender seus conhecimentos no campo da física, começando a trabalhar em problemas de física teórica, especialmente em mecânica, capilaridade, acústica, óptica e cristalografia, tendo como primeiro fruto destes trabalhos o "UBER EIN NEUES ALLGEMEINES GRUNDGESETZ DER MECHANIK".

Em 1830, Gauss publicou o "PRINCIPIA GENERALIA THEORIARE FIGURAE FLUIDORUM EN STATU AEQUILIBRII" que foi uma importante contribuição para o campo da capilaridade e teve um importante papel no cálculo de variações, pois foi a primeira solução envolvendo integrais duplas, condições de contorno e limites variáveis.

Em 1832 Gauss apresentou à Academia o "INTENSISITAS VIS MAGNECTICAE TERRESTRIS AD MENSURAM ABSOLUTAM REVOCATA", em que aparece pela primeira vez o primeiro uso sistemático de unidades absolutas (distância, massa, tempo) para medir grandezas não mecânicas.

Juntamente com Weber, em 1833, Gauss chegou às leis de Kirchoff e antecipou várias descobertas na eletricidade, estática, térmica e da fricção, porém não publicaram resultados, pois seus interesses estavam voltados ao eletromagnetismo terrestre, sendo que a publicação de maior relevância neste campo foi "ALLGEMEINE THEORIE DES ERMAGNETISMUS (1839)" no qual Gauss expressa o potencial em qualquer ponto da superfície da terra como uma série infinita de funções esféricas, juntamente com dados experimentais.

Gauss terminou suas pesquisas no campo da física com a publicação de "ALLGEMEINE LEHRSATSE IN BEZIEHUNG AUF DIE IM VERKEHRTEN VERHALTNISSE DES QUADRATS DER ENTFERNUNG WIRKENDEN ANZIEHUNGS UND ABSTOSSUNGSKRAFTE (1840)". No mesmo ano Gauss terminou o 'DIOPTRISCHE UNTERSUCHUNGEN (1841), no qual ele analisa o caminho da luz através de um sistema de lentes e mostrou entre outras coisas, que qualquer sistema é equivalente à escolha correta de uma única lente. Gauss dizia que esta teoria era de seu conhecimento a quarenta anos, porém ele as considerava muito elementares para serem publicadas, sendo que esta teoria foi tida como um de seus melhores trabalhos, por parte de um de seus maiores biógrafos.

ÚLTIMOS ANOS

Seus últimos anos foram cheios de honrarias mas não da felicidade que ele teria merecido. Pela primeira vez em mais de vinte anos ele deixou Göttingem, no dia 16 de Junho de 1854, para ver a estrada de ferro que estava sendo construída entre sua cidade e Kassel. Gauss sempre tivera agudo interesse pela construção e operação de estradas de ferro; agora ele veria uma sendo construída. No caminho, os cavalos dispararam; ele foi atirado para fora da carruagem. Não ficou ferido mas muito chocado. Recuperando-se, ainda teve o prazer de assistir à abertura das cerimônias quando a estrada de ferro chegou a Göttingen em 31 de Julho de 1854.

No começo do ano seguinte surgiram os sintomas de gota. Inteiramente consciente, praticamente até ao fim, morreu pacificamente na manhã de 23 de Fevereiro de 1855.

Referências:

20 de jun. de 2012

Em Matérias de Nível Médio, iremos falar de

PROGRESSÃO ARITMÉTICA (P.A)

Uma progressão aritmética a famosa P.A, é algo que sempre está nos pesadelos dos alunos.

Mas muita calma, meu caro, pois não é algo nada assustador, basta apenas um pequeno entendimento.

Uma P.A. consiste em uma sequência numérica com uma ordem de grandeza lógica, assim a variação de uma progressão de números consistirá numa sequência de números proporcionais.

Em outras palavras uma sequência de números do tipo:

2, 6, 10, 14, 18...

segue uma sequência lógica de crescimento, que no exemplo acima é de fácil percepção que este crescimento dá se num intervalo de 4, ou seja, uma P.A. é algo que vemos desde criança, muitas vezes em forma de brincadeira mas que obviamente não temos este conhecimento ainda.

Numa P.A. o termo central é a média aritmética, isto a partir do segundo termo, do termo antecessor pelo sucessor. Como no exemplo acima. Se fizermos a média de 2 e 10, verificamos que o resultado é 6, ou seja, o termo divisor entre os dois.

Bom, agora vamos para as definições matemáticas e especificações da P.A.

Razão de uma P.A (r)

Este crescimento linear que ocorre nesta sequência numérica, recebe um nome especifico, conhecido nas melhores casas do ramo como Razão, que em outras palavras, seria a diferença que existe de um número para outro.

A razão é definida pela letra r. No exemplo acima, nossa razão é igual a 4.

1, 3 , 5, 7, 9.... ( a razão neste exemplo é de 2)

2, 7, 12, 17... (razão igual a 5)

ou seja, o melhor método de se descobrir a razão de uma P.A. é fazer a diferença de um termo por seu antecessor:

r = an - (an-1)

A verificação da existência de uma razão é o que define uma P.A.

Classificação de uma P.A

Crescente - uma P.A. é crescente quando r >0 e, cada termo a partir do segundo é um termo maior do que seu antecessor, assim nossos exemplos anteriores podem ser definidos como uma, progressão aritmética crescente.

Decrescente - uma P.A é decrescente quando r<0 e, e cada termo a partir do segundo é menor que seu antecessor, segue o exemplo:

10, 7, 4, 1, -2 ....

Percebe-se que a razão existente nesta progressão é uma razão negativa, r = -3, assim é uma P.A. decrescente.

Constante - uma P.A constante é uma P.A na qual não existe uma razão, ou seja, r = 0, deste modo, pode verificar no exemplo:

5, 5, 5, 5, 5 .....

8, 8, 8, 8, 8.....

que é uma progressão constante, definido por uma razão nula.

De Segunda Ordem - é uma P.A mais complexa, pois a variação dos termos segue uma P.A, ou seja, sua lógica é um pouco mais elaborada, como:

1, 3, 7, 13, 21, 31, 43....

Consegue definir esta sequência?!

Pois é, a razão existente entre os termos é uma P.A, verifique que, o primeiro termo para o segundo a diferença é de 2, do segundo para o terceiro de 4, do terceiro para o quarto verificamos que a diferença passa a ser 6, ou seja, por esta análise, conclui-se que a progressão segue uma razão lógica, onde a diferença de um termo para o próximo varia de uma razão igual 2, assim sendo, a variação consiste em 2, 4, 6, 8 e assim por diante.

Com o estudo de P.A. de ordens superiores chega-se a introdução do cálculo de integrais de funções polinomiais.

Termo Geral de uma P.A.

Conhecida a razão de uma P.A. é possível definir seu termo geral, ou seja, qualquer termo em qual se queira conhecer, que é dado pela fórmula:

an = a1 + ( n - 1) * r

Assim, caso queira conhecer o enésimo termo de uma P.A. basta sabe seu primeiro termo dado por a1, o número de termos até an dado por n e a razão, deste modo segue no exemplo que se, caso queiramos conhecer o 20º termo da progressão, basta aplicarmos esta fórmula:

1, 4, 7, 10, 13 ...

an = 1 + ( 20 - 1) *3 = 58

Soma de Termos de uma P.A. finita

Para somarmos os termos de uma série finita em uma progressão dado um intervalo conhecido de ap até aq, poder-ei-mos aplicar a seguinte fórmula, a qual define a somatória de elementos de uma P.A.:

Sn = n * (a1 + an)/ 2

Também pode-se aplicar na fórmula a ideia de intervalo, assim:

S(p,q) = (q-p-1) * (aq + ap) / 2

Definido no intervalo fechado (p,q).

Curiosidade:

Diz a lenda que o grande matemático Carl Friedrich Gauss [veja artigo principal] em seus primórdios de vida, aos dez anos de idade, em uma atividade escolar feita por seu diretor, na qual consistia encontrar a soma dos números de 1 a 100, concluiu o exercício em poucos minutos, utilizando do princípio de P.A, fascinado com feito, o diretor começou a incentivá-lo nos estudos matemáticos, ali deu-se o pontapé para o grandes feitos deste grande matemático.

Referências:

http://www.brasilescola.com/matematica/progressoes-aritmeticas.htm

http://progressao.br.tripod.com/P.A..html

http://pt.wikipedia.org/wiki/Progress%C3%A3o_aritm%C3%A9tica

http://www.algosobre.com.br/matematica/progressao-aritmetica-pa.html